|
|
|
|
|
§ 3. Четыре замечательные точки треугольника Теорема о пересечении высот треугольникаМы доказали, что биссектрисы треугольника пересекаются в одной точке, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Ранее было доказано, что медианы треугольника пересекаются в одной точке (п. 64). Оказывается, аналогичным свойством обладают и высоты треугольника. Теорема
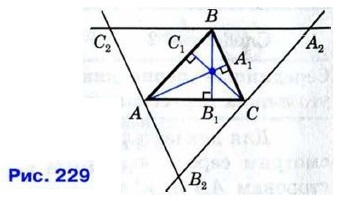
Доказательство Рассмотрим произвольный треугольник АВС и докажем, что прямые АА1 ВВ1 и СС1 содержащие его высоты, пересекаются в одной точке (рис. 229).
Проведём через каждую вершину треугольника АВС прямую, параллельную противоположной стороне. Получим треугольник А2В2С2. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ = А2С и АВ = СВ2 как противоположные стороны параллелограммов АВА2С и АВСВ2, поэтому А2С = СВ2. Аналогично С2А = АВ2 и С2В = ВА2. Кроме того, как следует из построения, СС1 ⊥ А2В2, АА1 ⊥ В2С2 и ВВ1 ⊥ А2С2. Таким образом, прямые АА1, ВВ1 и СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2. Следовательно, оНи пересекаются в одной точке. Теорема доказана. Итак, с каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений). Эти четыре точки называются замечательными точками треугольника.
|
|
|